A linear-feedback shift register (LFSR) is a shift register whose input bit is a linear function of its previous state.
The most commonly used linear function of single bits is exclusive-or (XOR). Thus, an LFSR is most often a shift register whose input bit is driven by the XOR of some bits of the overall shift register value.
Two implementation methods are usually considered:
- Simple shift register generator (SSRG) or Fibonacci configuration
- Modular shift register generator (MSRG) or Galois configuration
Fibonacci Configuration
The following two diagrams illustrate the Fibonacci configurations of LFSR with register shifting direction to LSB/Right and MSB/Left, respectively.
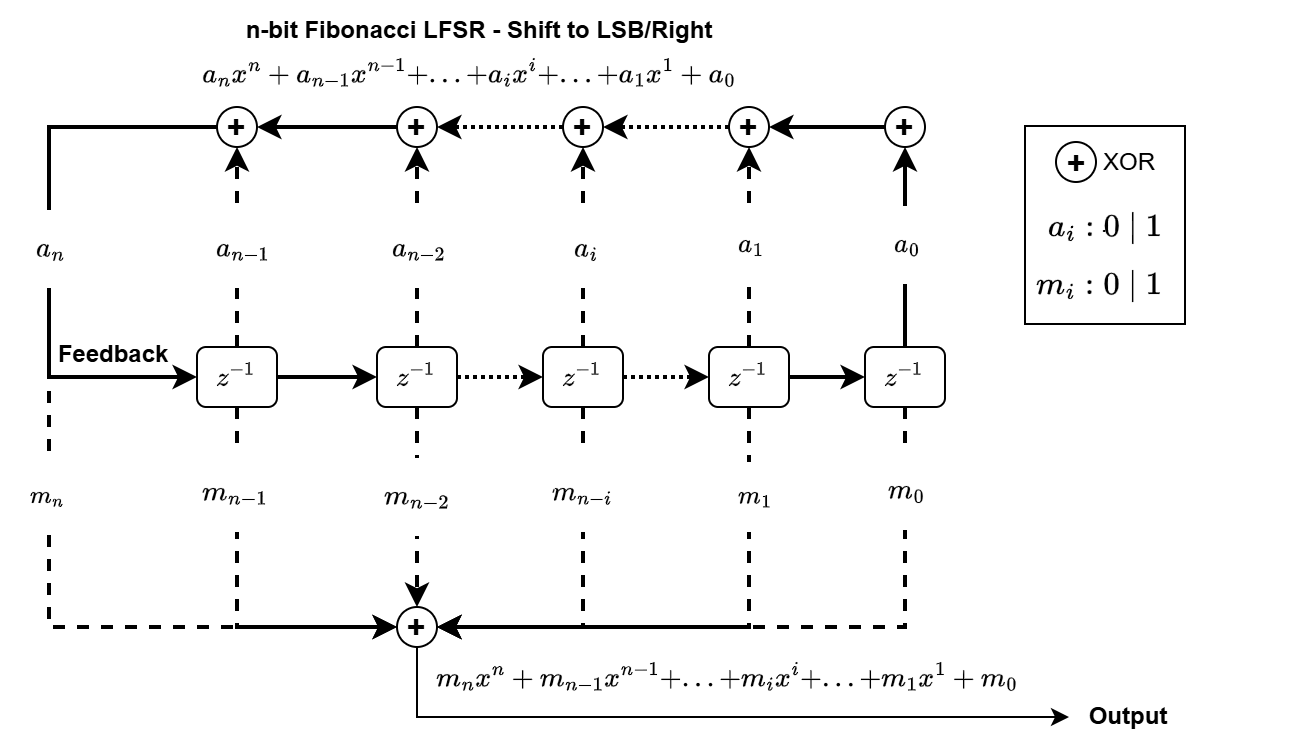
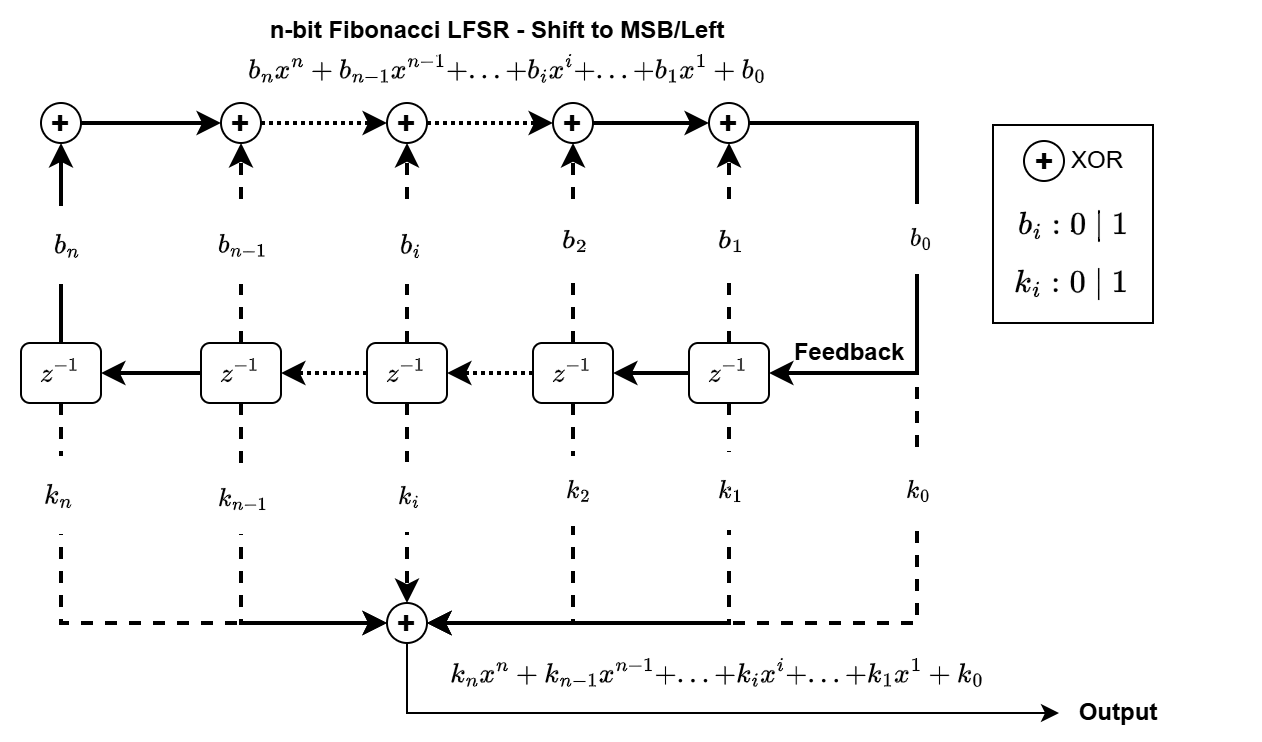
The polynomial \(a\) or \(b\) determines the feedback connections of the shift register. It is a primitive binary polynomial in \(x\), \(a_nx^n+a_{n–1}x^{n–1}+...+a_2x^2+a_1x^1+a_0\) or \(b_nx^n+b_{n–1}x^{n–1}+...+b_2x^2+b_1x^1+b_0\). For the coefficient \(a_{i}\) or \(b_{i}\), the coefficient is 1 if there is a connection from the ith register to the adder. The leading term, \(a_n\) or \(b_n\), and the constant term, \(a_0\) or \(b_0\), of the generator polynomial must be 1 because the polynomial must be primitive. At each time step, all n registers in the generator update their values according to the value of the incoming arrow to the shift register. The adders perform addition modulo 2. The output of the LFSR reflects the sum of all connections in the m or k mask vector.
The m or k mask vector is optional. The output bit will be the bit shifted from the final register at the shift direction if a mask vector is not provided.
The two Fibonacci configurations are equivalent if \(a_i=b_{n-i}\) and the initial seeds are mirror imaged. For example, the maximum length sequence for a 7-bit LFSR should have \(a_i=1\) at (7, 6, 0) and \(b_i=1\) at (7, 1, 0).
Note
The tap indices start from the right most position in the LFSR.
Galois Configuration
The following two diagrams illustrate the Galois configurations of LFSR with register shifting direction to MSB/Left and LSB/Right, respectively.
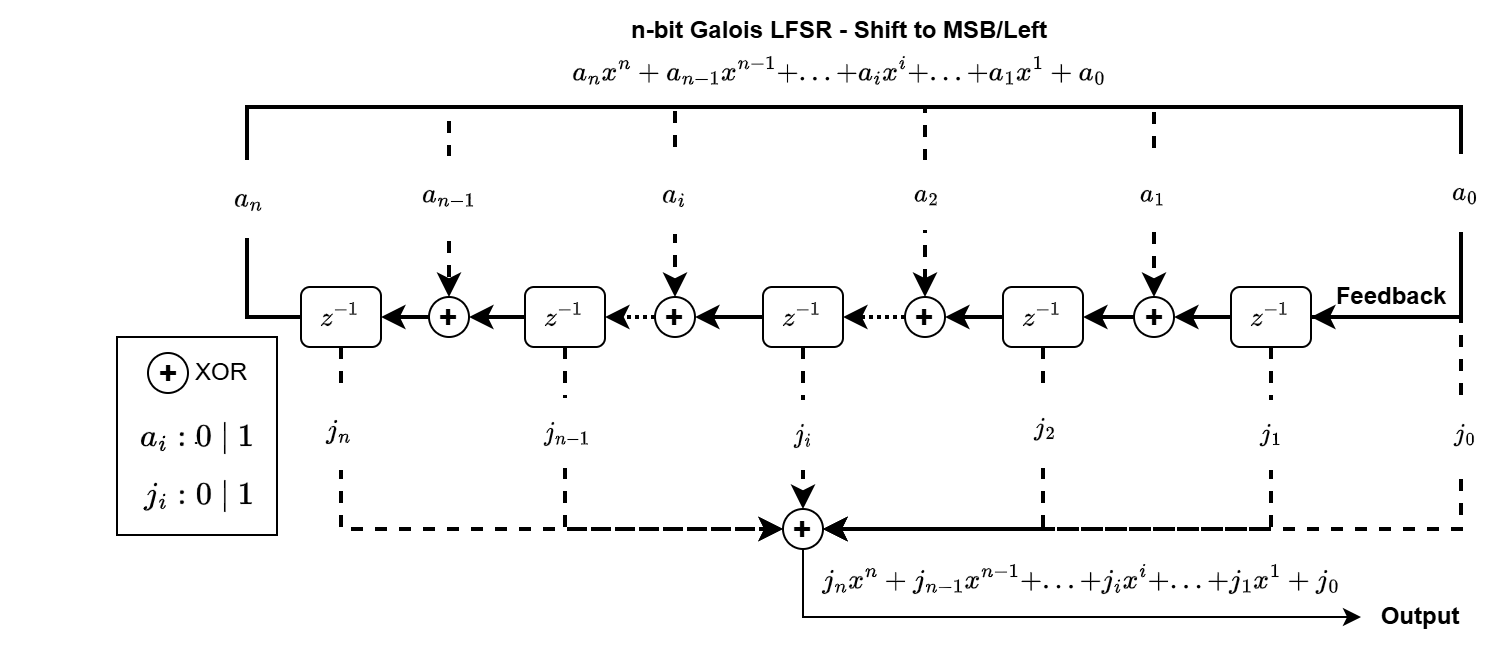
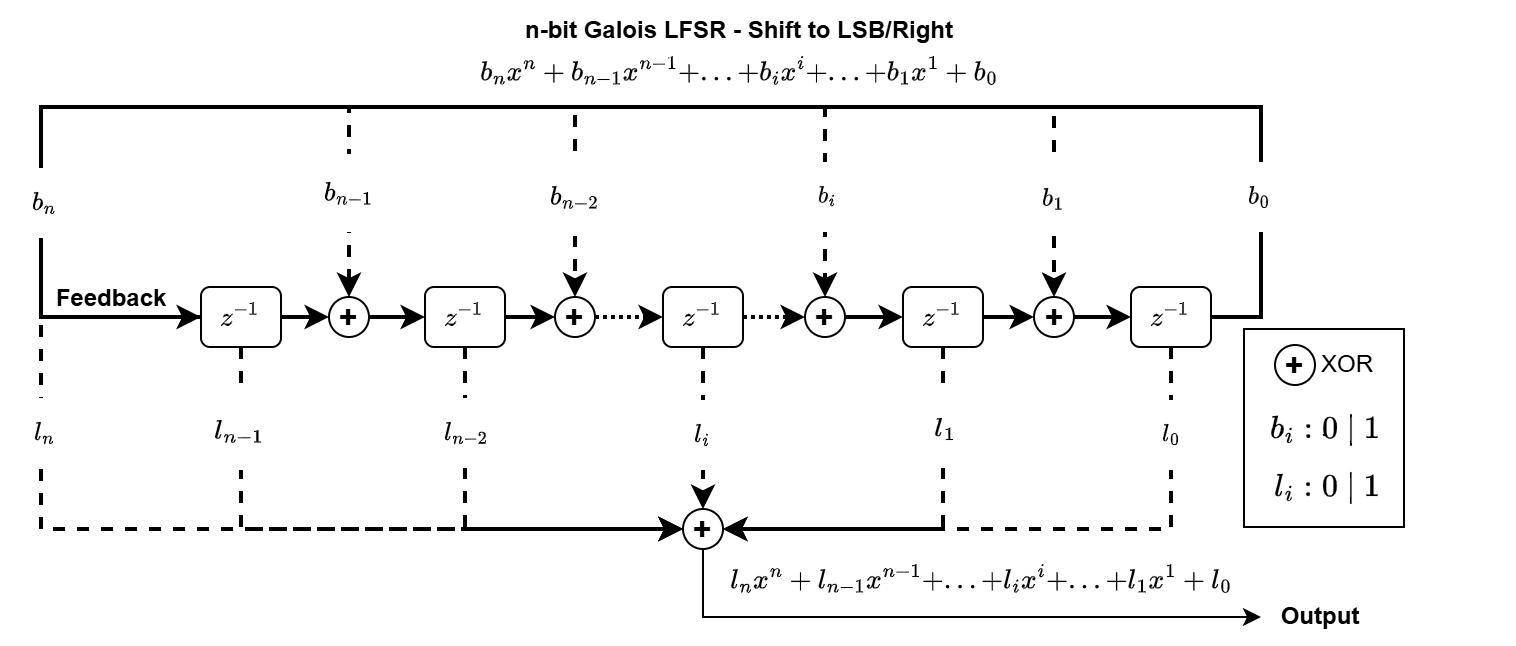
The Galois LFSR has the same output stream as the Fibonacci LFSR with a time/phase offset. So a different start point will be needed to get the same output each cycle.
Coefficients of Galois LFSR shifting to MSB should be identical as Fibonacci LFSR shifting to LSB to generate the same sequence with a phase offset. Similarly for Galois LFSR shifting to LSB and Fibonacci shifting to MSB.
Maximum Length Sequence (MLS)
The maximum sequence length is \(2^n – 1\). MLS have the following properties.
Balance Property
The occurrence of 0 and 1 in the sequence should be approximately the same. More precisely, in a maximum length sequence of length \(2^n-1\) there are \(2^{n-1}\) ones and \(2^{n-1}-1\) zeros. The number of ones equals the number of zeros plus one, since the state containing only zeros cannot occur.
Run Property
A "run" is a sub-sequence of consecutive "1"s or consecutive "0"s within the MLS concerned. The number of runs is the number of such sub-sequences.
Of all the "runs" (consisting of "1"s or "0"s) in the sequence :
- One half of the runs are of length 1.
- One quarter of the runs are of length 2.
- One eighth of the runs are of length 3.
- ... etc. ...
Correlation Property
The circular autocorrelation of an MLS is a Kronecker delta function (with DC offset and time delay, depending on implementation). For the \(\pm 1\) convention, i.e., bit value 1 is assigned \(s=+1\) and bit value 0 \(s=-1\), mapping XOR to the negative of the product:
where \(s^*\) represents a complex conjugate and \([m+n]_N\) represents a circular shift.
The linear autocorrelation of an MLS approximates a Kronecker delta.
To generate a maximum length sequence for a generator polynomial that has the degree n, set Polynomial to a value from the following table. The table is applied to Fibonacci Shifting to LSB and Galois Shifting to MSB configurations. Counterpart values of \(n-i\) should be used for the other two configurations.
| n | Generator Polynomial | n | Generator Polynomial | n | Generator Polynomial | n | Generator Polynomial |
|---|---|---|---|---|---|---|---|
| 2 | [2 1 0] | 15 | [15 14 0] | 28 | [28 25 0] | 41 | [41 3 0] |
| 3 | [3 2 0] | 16 | [16 15 13 4 0] | 29 | [29 27 0] | 42 | [42 23 22 1 0] |
| 4 | [4 3 0] | 17 | [17 14 0] | 30 | [30 29 28 7 0] | 43 | [43 6 4 3 0] |
| 5 | [5 3 0] | 18 | [18 11 0] | 31 | [31 28 0] | 44 | [44 6 5 2 0] |
| 6 | [6 5 0] | 19 | [19 18 17 14 0] | 32 | [32 31 30 10 0] | 45 | [45 4 3 1 0] |
| 7 | [7 6 0] | 20 | [20 17 0] | 33 | [33 20 0] | 46 | [46 21 10 1 0] |
| 8 | [8 6 5 4 0] | 21 | [21 19 0] | 34 | [34 15 14 1 0] | 47 | [47 14 0] |
| 9 | [9 5 0] | 22 | [22 21 0] | 35 | [35 2 0] | 48 | [48 28 27 1 0] |
| 10 | [10 7 0] | 23 | [23 18 0] | 36 | [36 11 0] | 49 | [49 9 0] |
| 11 | [11 9 0] | 24 | [24 23 22 17 0] | 37 | [37 12 10 2 0] | 50 | [50 4 3 2 0] |
| 12 | [12 11 8 6 0] | 25 | [25 22 0] | 38 | [38 6 5 1 0] | 51 | [51 6 3 1 0] |
| 13 | [13 12 10 9 0] | 26 | [26 25 24 20 0] | 39 | [39 8 0] | 52 | [52 3 0] |
| 14 | [14 13 8 4 0] | 27 | [27 26 25 22 0] | 40 | [40 5 4 3 0] | 53 | [53 6 2 1 0] |
Comments